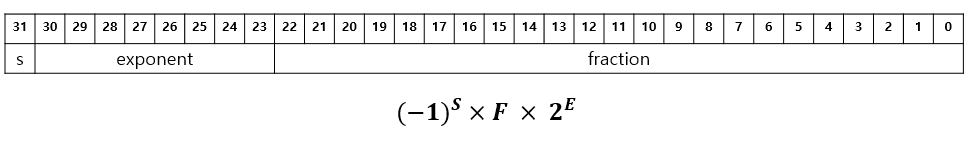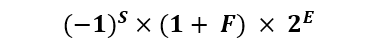컴퓨터 구조 및 설계 3장

3장 컴퓨터 연산

3.2 덧셈과 뺄셈

오버플로가 발생하지 않는 경우

• 덧셈에서 부호가 다른 피연산자를 더할 경우
  • 두 피연산자 중 어느 하나보다는 커질 수 없기 때문
• 뺄셈에서는 부호가 같을 경우
  • 같은 부호의 수를 빼는 것 = 부호가 다른 수를 더하는 것

오버플로가 발생하는 경우

• 올림수가 부호 비트로 올라간 경우
  • 두 양수를 더한 값이 음수가 되는 경우
  • 두 음수를 더했는데 합이 양수가 되는 경우
• 부호 비트에서 빌림수가 발생한 경우
  • 양수에서 음수를 뺀 결과가 음수인 경우
  • 음수에서 양수를 뺀 결과가 양수인 경우

MIPS는 오버플로를 탐지하면 예외(exception)를 발생시킨다. 예외를 인터럽트(interrupt)라고 부르기도 한다. 오버플로가 발생한 명령어의 주소는 레지스터에 저장되고, 컴퓨터는 적절한 처리를 하기 위해서 해당 루틴으로 점프한다. 인터럽트가 걸린 주소를 저장해, 해당 처리를 한 다음에 프로그램 실행을 계속할 수 있게 한다.
MIPS에는 EPC(Exception Program Counter)라고 불리는 레지스터가 있어 인터럽트가 걸린 명령어의 주소를 기억하는데 이용된다. mfc0(move from system control) 명령어는 EPC를 범용 레지스터에 복사해, MIPS 소프트웨어가 점프 레지스터 명령어를 통해 인터럽트가 걸린 명령어로 되돌아갈 수 있게 해준다.

3.3 곱셈

• 피승수(multiplicand): 첫 번째 피연산자
• 승수(multiplier): 두 번째 피연산자
• 곱(product): 최종 결과

곱셈 알고리즘과 하드웨어의 순차적 버전

1. 승수의 최하위 비트를 통해 피승수를 곱 레지스터에 더할지 말지를 결정한다.
   • 승수의 자리 수가 1이면 피승수를 곱에 더한다.
   • 승수의 자리 수가 0이면 2단계로 넘어간다. (0이기 때문)
2. 피승수를 왼쪽으로 자리이동한다.
3. 승수를 오른쪽으로 자리이동한다.

ex) 4비트 수 0010 _ 0011를 구하라 여기서 피승수 레지스터, 곱 레지스터는 8비트이지만, 승수 레지스터는 4비트이다. 피승수는 승수의 비트만큼 왼쪽으로 이동해야하기 때문에, 피승수의 비트 4 + 승수의 비트 4 = 총 8비트가 필요하다. 또한, 곱 레지스터에 피승수를 더하기 때문에 동일하게 8비트를 가진다.

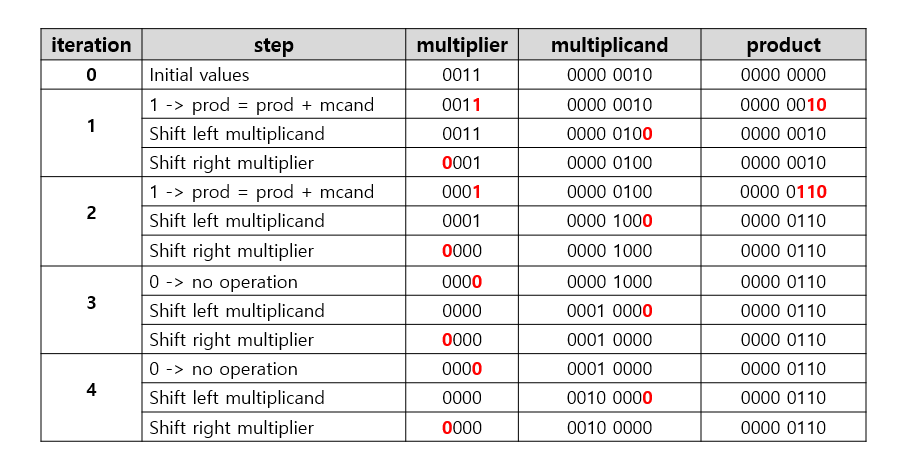
이 알고리즘과 하드웨어는 매 반복이 한 클럭 사이클만 걸리도록 쉽게 바꿀 수 있다. 연산을 병렬로 수행함으로써 속도 향상이 가능해진다. 승수 비트가 1일 때 피승수를 곱에 더하는 동안 승수와 피승수를 자리이동한다. 덧셈기와 레지스터에서 사용되지 않는 부분이 있기 때문에 폭을 절반으로 줄여(64bit -> 32bit) 더욱 최적화할 수 있다. 또한, 곱 레지스터가 64bit일 경우 승수를 곱 레지스터의 오른쪽 절반에 놓을 수 있다.

부호있는 곱셈

승수와 피승수를 양수로 변환해 계산하고, 피연사자들의 부호가 서로 다를 때만 곱을 음수로 바꾼다.

더 빠른 곱셈

승수의 32개 비트 각각을 조사하면, 곱셈을 시작하는 초기에 이미 피승수가 더해져야 하는지 아닌지를 알 수 있다. 즉, 승수의 매 비트마다 32비트 덧셈기를 하나씩 할당하면 더 빠른 곱셈이 가능하다.

여러 방법들

1. 덧셈기의 한 입력은 피승수를 해당 승수 비트와 AND한 것이고 다른 입력은 앞 덧셈기의 출력이다.
2. 오른쪽 덧셈기의 출력을 왼쪽 덧셈기의 입력에 연결하여 32층의 덧셈기 스택을 만든다.
3. 32번의 덧셈을 병렬 트리구조로 만든다.

MIPS에서의 곱셈

• mult: 부호가 있는 곱셈
• multu: 부호가 없는 곱셈
• mflo(move from lo)/mfhi(move from hi): 32비트 정수 곱을 범용 레지스터로 가져옴

multu 수행 결과 Hi가 0이거나, mult 수행결과 Hi가 Lo의 부호와 같은 비트 32개로 채워져 있다면, 오버플로가 아니다.

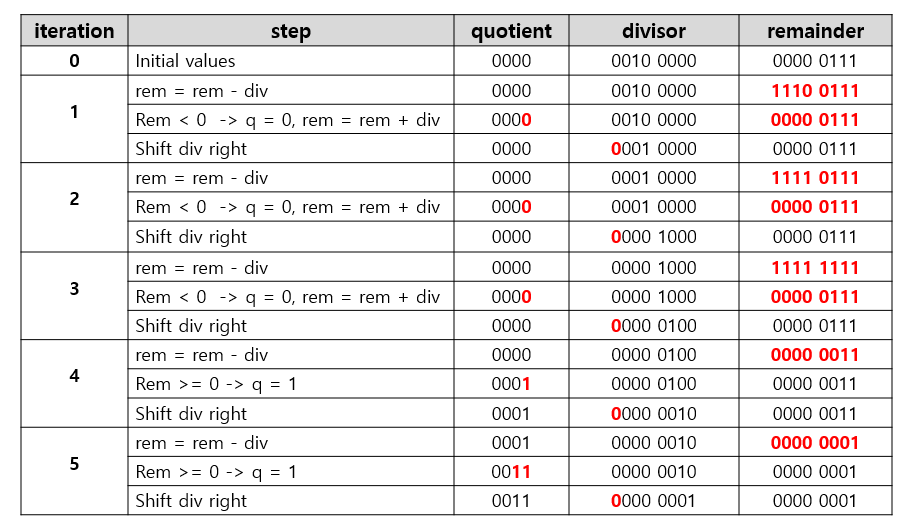
3.4 나눗셈

• 피제수(dividend): 나누어지는 수
• 제수(devisor): 피제수를 나누는 수
• 피제수 = 몫 * 제수 + 나머지

나눗셈 알고리즘과 하드웨어

1. 레지스터를 초기화한다.
   • 몫(Quotient) 레지스터 32비트를 0으로 초기화해서 시작한다.
   • 제수는 매번 오른쪽으로 한 비트씩 자리이동시켜야 하기 때문에 64비트 제수 레지스터의 왼쪽 절반에 넣고 시작한다.
   • 나머지 레지스터는 피제수로 초기화된다.
2. 피제수 - 제수 결과값을 나머지 레지스터에 넣는다.
   • 제수가 피제수보다 작거나 같은지 확인하기 위해
3. 나머지 값이 양수인 경우 A, 음수인 경우 B
   • A: 몫에 1을 넣는다.
   • B: 몫에 0을 넣고 제수를 나머지 레지스터에 다시 더함으로써 원래의 값을 회복한다.
4. 제수는 오른쪽으로 자리이동한다.

ex) 4비트 수 0000 0111 나누기 0010를 구하라

이 알고리즘과 하드웨어는 훨씬 더 빠르고 싸게 개선될 수 있다. 뺄셈과 동시에 피연산자의 몫을 자리이동시키면 성능 향상이 가능하다. 레지스터와 덧셈기에 사용되지 않는 부분이 있음을 활용하여 덧셈기와 레지스터 크기를 절반으로 줄일 수 있다. 또한, 몫 레지스터를 나머지 레지스터의 오른쪽 절반에 결합시켰다.

부호있는 나눗셈

제수와 피제수의 부호를 기억하고 이 부호들이 다른 경우에는 몫을 음수화한다.

나머지의 부호

두 연산자의 부호가 다를 경우에는 몫의 부호를 음수로 하고, 나머지가 0이 아니면 나머지의 부호는 피제수의 부호를 따르게 한다.

더 빠른 나눗셈

나눗셈에서는 다음 단계를 수행하기 전에 뺄셈한 결과의 부호를 알아야 하기 때문에 곱셈과 같이 많은 수의 덧셈기를 사용해 속도를 빠르게 할 수 없다.

SRT 나눗셈은 각 단계에서 여러 개의 몫 비트를 예측하는 기법을 사용한다. 피제수와 나머지의 상위 비트들을 이용하여 표를 찾아서 몫을 추측하고, 틀린 추측은 그 후의 단계에서 바로잡는다.

MIPS에서의 나눗셈

나눗셈 명령이 완료된 뒤 Hi는 나머지, Lo는 몫을 갖는다.

• div(divide): 부호있는 나눗셈
• divu(divide unsigned): 부호없는 나눗셈
• mflo/mfhi: 원하는 결과를 범용 레지스터에 넣는다.

나눗셈 알고리즘 종류

1. 비복원(nonrestoring) 나눗셈
   • 나머지가 음수인 경우, 음수 그대로 두고 다음 단계에서 자리이동된 나머지에 피제수를 더하는 방법
   • 각 단계마다 1사이클씩 소요
2. 복원(restoring) 나눗셈
   • 위에서 설명한 것과 같이 나머지가 음수인 경우, 제수를 바로 더해 원상 복구한다.
3. 조건부실행(nonperforming) 나눗셈
   • 뺄셈의 결과가 음수이면 이를 저장하지 않는다.
   • 평균적으로 1/3배 만큼 적은 수의 산술연산을 한다.

3.5 부동소수점

• 과학적 표기법(scientific notation)
  • 소수점의 왼쪽에는 한 자리 수만 있다.
  • ex) 0.1 * 10^6
• 정규화된 수(normalized number)
  • 과학적 표기법으로 표현된 숫자 중 맨 앞에 0이 나오지 않는 수
  • ex) 1.0 * 10^2

부동소수점(floating point)는 소수점의 위치가 고정되어 있지 않은 수를 말한다.

실수를 정규화된 형태의 표준 과학적 표기법으로 나타내면 좋은 점

1. 부동소수점 숫자를 포함한 자료의 교환을 간단하게 한다.
2. 부동소수점 산술 알고리즘이 간단해진다.
   • 숫자가 항상 이런 형태로 표현된다는 것을 알고 있기 때문
3. 한 워드 내에 저장할 수 있는 수의 정밀도를 증가시킨다.
   • 불필요하게 선행되는 0을 소수점 오른쪽에 있는 실제 숫자로 바꾸기 때문

부동소수점 표현

• 소수부분(fraction)과 지수(exponent)의 크기 사이에서 타협점을 찾아야 한다.
  • 고정된 워드 크기를 사용하기 때문에 하나를 증가시키면 다른 하나를 감소시켜야 하기 때문이다.
    • 소수부분의 크기를 증가시키면, 정밀도가 높아진다.
    • 지수의 크기를 증가시키면, 수의 범위가 늘어난다.

• 부호: 1비트 (0: 양수, 1: 음수)
• 지수: 8비트 (지수의 부호 포함)
• 소수: 23비트

부호와 크기(sign and magnitude) 표현 방식

부호가 수의 나머지 부분과 떨어져 독립된 비트로 표현된다.

표현할 수 있는 수의 범위가 정해져있기 때문에 발생하는 문제

1. 오버플로(overflow)
   • 지수가 너무 커서 지수 필드에 들어갈 수 없는 경우
2. 언더플로(underflow)
   • 음수 지수의 절대값이 너무 커서 지수 부분에 표현될 수 없는 경우

2배 정밀도(double precision) 부동소수점 연산

• 언더플로, 오버플로의 발생 가능성을 줄이는 방법
• 지수 부분이 더 큰 다른 표현 형식을 사용한다.

• 부호: 1비트
• 지수: 11비트
• 소수: 52비트
• 장점
  • 지수의 범위를 크게 해준다.
  • 더 큰 유효자리를 제공하여 정밀도를 높인다.

IEEE 754 부동소수점 표준

• 정규화된 이진수의 가장 앞쪽 1비트를 생략하고 표현하지 않는다.

  • 유효자리 부분에 더 많은 수를 담기 위해
  • 실제적인 유효자리는 단일 정밀도 표현에서는 24비트의 길이, 2배 정밀도 표현에서는 53비트의 길이를 가진다.
  • 유효자리(significand): 숨겨진 1과 소수 부분

  

• 숫자 0.0은 선행하는 1이 없기 때문에, 예약된 지수 값 0을 가진다.
  • 하드웨어는 선행하는 1을 붙이지 않는다.
• 비정상적인 사건을 표현하는 특수 심벌이 있다.
  • 무한대: 표현 가능한 가장 큰 지수 값을 사용한다.
  • NaN: 0 나누기 0 이나 무한대 빼기 무한대와 같은 유효하지 않은 연산의 결과를 위한 심벌
• 부호 비트를 최상위 비트에 놓아 쉽게 정렬될 수 있는 부동 소수점 표현

바이어스된 표현법(biased notation)

• 양수 지수의 경우, 지수가 큰 수가 지수가 작은 수보다 더 큰 정수처럼 보인다.
• 음수 지수의 경우, 2의 보수법이나 지수의 최상위 비트를 1로 만드는 표현법을 사용한다면, 지수가 음수이면 양수 지수보다 큰 수처럼 보일 것이다.

이를 해결하기 위해 가장 음수인 지수는 00…000로, 가장 양수인 지수를 11…111로 표현하는 방식이다.
여기서 바이어스는 실제값을 구하기 위해 부호없이 표현된 수에서 빼야하는 상수를 말한다.

IEEE 754의 단일 정밀도 표현 방식에서는 바이어스 값 127을 사용한다. 2배 정밀도를 위한 지수의 바이어스는 1023이다.

부동소수점 덧셈

1. 작은 수의 유효자리를 지수가 큰 수의 것과 일치할 때까지 오른쪽으로 자리이동시킨다. 자리이동 후 유효자리 수만큼 자른다.
2. 유효자리를 서로 더한다.
3. 오버플로와 언더플로를 검사하면서, 정규화 형태로 만들기 위해 지수를 적절하게 조절하고 합을 자리이동시켜야한다.
4. 유효자리만큼 수를 자리맞춤(rounding)해야 한다.

부동소수점 곱셈

1. 바이어스된 지수를 서로 더한 후, 바이어스 하나를 빼서 곱의 새 지수를 구한다.
2. 유효자리의 곱셈을 구한다.
3. 오버플로와 언더플로를 검사하면서, 정규화 형태로 만들기 위해 곱셈 후의 결과를 자리이동한다.
4. 유효자리에 맞게 자리맞춤한다.
5. 결과의 부호는 원래 피연산자의 부호에 의존한다. 부호가 같으면 양수, 그렇지 않으면 음수이다.

MIPS의 부동소수점 명령어

ex) 부동소수점 변수 fahr는 $f12로 전달되고 결과는 $f0에 저장된다고 가정하자.

float f2c(float fahr) {
    return ((5.0 / 9.0) * (fahr - 32.0));
}

컴파일러가 전역 포인터 $gp로 쉽게 접근할 수 있는 거리에 부동소수점 상수 3개를 넣는다.

f2c:
    lwcl $f16, const5($gp)      # $f16 = 5.0
    lwcl $f18, const9($gp)      # $f18 = 9.0

    div.s $f16, $f16, $f18      # $f16 = (5.0 / 9.0)

    lwcl $f18, const32($gp)     # $f18 = 32.0
    sub.s $f18, $f12, $f18      # $f12 = (fahr - 32.0)

    mul.s $f0, $f16, $f18       # $f0 = (5.0 / 9.0) * (fahr - 32.0)
    jr $ra                      # return

정확한 산술

정확하게 자리맞춤하기 위해서는 계산할 때 하드웨어가 추가 비트를 포함하여야 한다.
IEEE 754는 계산하는 동안 오른편에 항상 두 개의 추가 비트를 유지한다. 이를 각각 보호 비트(guard bit)와 자리맞춤 비트(round bit)라고 부른다.

자리맞춤 시 최악의 경우는 실제 값이 두 부동소수점 표현의 중간이 될 때이다. 부동소수점에서 정확도는 유효자리의 최하위 비트 중 오류가 발생한 것이 몇비트인가에 따라 결정된다. 이 척도를 ulp(units in the last place)라고 부른다.

3.6 병렬성과 산술연산: 서브워드 병렬성

큰 워드 내부에 병렬성이 있다고 할 때, 이것의 확장을 서브워드 병렬성이라고 한다. 더 일반적인 이름으로 데이터 수준 병렬성이라고도 한다. 벡터 또는 SIMD(Single Instruction, Muliple Data)라고도 한다.

3.7

3.8

3.9 오류 및 함정

오류: 한 비트 왼쪽 자리이동 명령어가 2를 곱해 준것과 같은 결과를 보이듯이 오른쪽 자리이동 명령어는 2로 나누어 준 것과 같은 결과를 나타낸다.

이는 부호없는 정수(unsigned integer)에서는 맞는 말이다. 하지만, 부호있는 정수(signed integer)인 경우에는 문제가 있다.

-5를 2의 보수법으로 표현하면, 1111 1111 1111 1111 1111 1111 1111 1011과 같다. 이를 2비트 오른쪽으로 자리이동하면, 0011 1111 1111 1111 1111 1111 1111 1110이다. 부호 비트가 0이 되므로 실제 기대했던 -1이 아닌 1,073,741,822가 된다.

이를 해결하기 위해 0을 채우는 대신 부호 비트를 채우는 산술적(arithmetic) 우측이동을 한다. 결과는 1111 1111 1111 1111 1111 1111 1111 1110이 된다. 즉, -2가 되었다. 근접하지만 맞는 값은 아니다.

함정: 부동소수점의 덧셈은 결합법칙이 성립하지 않는다.

부동소수점 수는 실수의 근사치이고 컴퓨터 연산도 제한된 정밀도를 갖기 때문에 부동소수점 수에서는 결합법칙이 성립하지 않는다. 문제는 부호가 다른 두 개의 매우 큰 수의 덧셈에 어떤 작은 수를 더할 때 발생한다.

a = 1.5 _ 10^38, b = -1.5 _ 10^38, c = 1.0일 때,

• a + (b + c) = 1.5 _ 10^38 + (-1.5 _ 10^38 + 1.0) = 1.5 _ 10^38 + (-1.5 _ 10^38) = 0.0
• (a + b) + c = (1.5 _ 10^38 + -1.5 _ 10^38) + 1.0 = (0.0) + 1.0 = 1.0

오류: 정수 데이터형에서 사용되는 병렬 수행 방식은 부동소수점 데이터형에도 똑같이 적용된다.

프로그램은 일반적으로 병렬로 수행되는 것을 작성하기 전에 순차적 수행 버전이 작성된다. 만약 두 결과가 같지 않으면, 병렬 버전이 문제가 있다고 생각할 수 있다. 이 방식은 컴퓨터 연산이 순차적 수행에서 병렬 수행으로 바뀌어도 결과에 영향을 미치지 않음을 가정한다. 즉, 100만개의 수를 더한다면 한 개의 프로세서를 사용한 것과 1000개의 프로세서를 사용한 것은 같은 결과를 얻게 된다.

2의 보수법을 사용하는 정수이면 정수 덧셈은 결합 법칙이 유효하므로 이 가정은 항상 옳다. 하지만, 부동소수점 덧셈은 결합법칙이 성립하지 않으므로 이 가정을 옳지 않다. 어떤 프로그램들이 같이 실행되느냐에 따라 병렬 컴퓨터의 운영체제 스케줄러가 프로세서 수를 다르게 할당하면 더 심각한 문제가 발생한다. 매번 부동소수점 합 계산 순서가 달라져서, 같은 입력에 같은 프로그램이 실행되더라도 약간씩 다른 결과가 나오게 될 것이다.

그렇기 때문에 부동소수점 수를 다루는 병렬 코드를 작성하는 프로그래머는 병렬 프로그램의 결과가 순차 프로그램과 똑같지 않을 때 이 값이 과연 믿을 만한 값인지 검증할 필요가 있다. 이를 다루는 분야를 수치해석이라고 한다.

함정: MIPS 명령어 addiu(add immediate unsigned)는 16비트의 수치 필드를 부호확장하여 사용한다.

MIPS는 수치를 사용하는 뺄셈 명령어를 지원하지 않으므로 음수는 부호확장되어야 한다.

오류: 이론 수학자만이 부동소수점 연산의 정확성에 신경을 쓴다.

Intel 엔지니어들이 절대 사용되지 않을 것으로 생각한 원소 5개 있었다. Intel이 Pentium을 만들면서 이것을 2 대신 0이 되게 PLA를 최적화하였다. 그래서 결과 중 앞부분 11비트는 항상 맞지만, 12번째~52번째 비트 사이에서 가끔씩 에러가 발생했다.

해당 버그를 수학교수인 Thomas Nicely가 발견하여 문의했지만 공식적인 답변을 듣지 못했다. 그는 이 사실을 인터넷에 올렸고, Intel은 이 버그를 이론 수학자에게만 영향을 미칠 사소한 결함이라고 불렀다. 일반 스프레드시트 사용자는 27,000년에 한 번꼴로 에러가 발생할 것이라고 했다. IBM 연구자들은 곧 일반 스프레드시트 사용자가 24일마다 한 번씩 이 에러를 보게 될 것이라고 주장하였다. 이에 Intel은 현재 출시 중인 Pentium프로세서를 오류가 없는 개선된 것으로 바꿔준다고 발표하고 굴복하였다.